
If you substitute n for 1, the common ratio would not be multiplied to the power of 0. For example, if you want to find out the 56 th term, you need to multiply by the power of 55. In this case, since you need to subtract 1 from 1 to get 0, you can think of it as the n th term is actually multiplied to the power of n-1. However, you can’t figure out the n th term just by looking at what n equals. The first term and common ratio do stay the same in this case, and in this example the first term is 3 and the common ratio is 5⁄ 9. So if n equaled 2, the exponent would be n-2, if n equaled 3, the exponent would be n-3, and so on. That’s because in an infinite geometric series, the first term must always be multiplied to the power of 0.
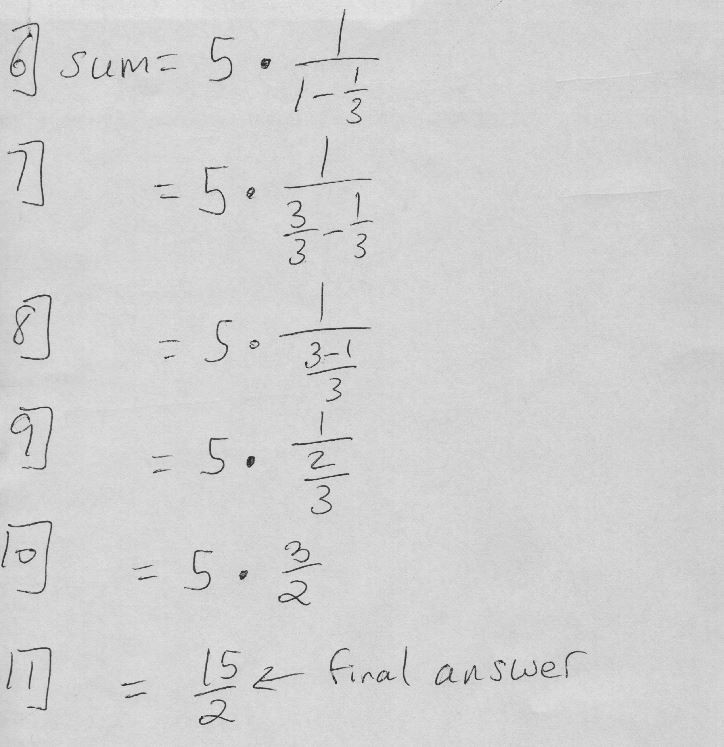
The first thing you’ll notice is that n equals 0 instead of 1, and the common ratio is being multiplied to the power of n as opposed to n-1. Sometimes you might an expression in this form:
Therefore, the 17 th term is approximately 0.5629.Įxpressions in Different Notations For instance, using the example presented above, let’s say we want to find the 17 th term of the series.
#Convergent geometric series series#
If you want to find a specific term for a series (2 nd term, 57 th term, 138 th term, etc.) in this format, just simply substitute the variable n for the number associated with the term. Therefore, in this equation, the sum of the series is 10.
Going off of this, if we use the expression, a⁄ 1-r, we would get 2⁄ (1-4/5) = 2⁄ 1/5 = 10. We can immediately see that the first term is 2 and the common ratio is 4⁄ 5, judging by which value was substituted for which variable. We could keep going and would see that the sum gets closer and closer to, but does not ever go over 20. How do we know that all of this is legitimate? If we look at the example above and manually calculate the terms one by one using the common ratio, we would get the following:Ī 1 + a 1r + a 1r 2 = 10 + 5 + 5⁄ 2 = 17.5Ī 1 + a 1r + a 1r 2 + a 1r 3 = 10 + 5 + 5⁄ 2 + 5⁄ 4 = 18.75Ĭontinuing this pattern, we will get the following sums: In this case, the sum of this series is 20. The values in the series keep getting progressively smaller, and thus, the series will eventually add up to a definitive sum. However, in something like "10 + 5 + 5⁄ 2 + 5⁄ 4 + …", the common ratio is 1⁄ 2. You can see that as the series continues infinitely, the values keep getting larger and we can’t get to a definitive sum. In this case, the common ratio would be 2. For example, let's look at the series of "10 + 20 + 40 + 80 + …". If |r| > 1, the series is divergent, as the sequence diverges and the values keep getting consecutively larger, so the sum will eventually reach infinity (and thus there will be no definitive sum). The general formula for this is on the right, where a = the first term, r = the common ratio, and r ≠ 0, 1.Īn infinite geometric series with a definitive sum is called a convergent series, as the sequence of the sum converges closer to a particular value. Oftentimes the series may be presented in sigma notation. To find the common ratio, use the formula: a 2⁄ a 1, where a 2 is the second term in the series and a 1 is the first term in the series. The general formula for finding the sum of an infinite geometric series is s = a 1⁄ 1-r, where s is the sum, a 1 is the first term of the series, and r is the common ratio. As the sequence goes on, the terms are getting smaller and smaller, slowly approaching zero.įinding the Sum of Infinite Geometric Series

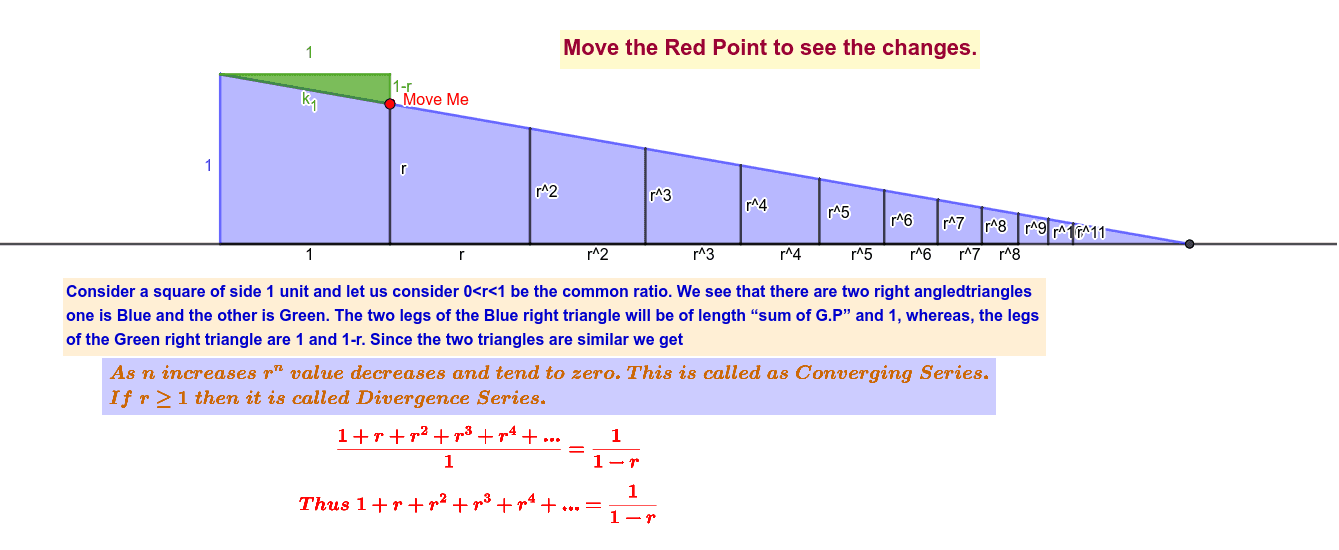
When the ratio has a magnitude greater than 1, the terms in the sequence will get larger and larger, and if you add larger and larger numbers forever, you will get infinity for an answer. The common ratio is a value for which the values in a series gets consistently multiplied by. Infinite geometric series can be written in the general expression: a 1 + a 1r + a 1r 2 + a 1r 3 + … + a 1r ∞, where a 1 is the first term and r is the common ratio. 2 Finding the Sum of Infinite Geometric Series.


 0 kommentar(er)
0 kommentar(er)
